- - Si lanzamos una pelota contra una pared aquella rebota. Hay una variación brusca del vector velocidad de la pelota en el instante del choque debido a la existencia de una fuerza muy intensa y de muy pequeña duración.Esta fuerza es debida a la deformación de la pelota en el corto intervalo de tiempo que dura el choque.
- - Si sobre un tapete de billar, ponemos una única bola, y con un taco damos un impulso a la bola, ésta cambia instantáneamente su velocidad iniciando su movimiento, pero, a partir de entonces, su velocidad ira disminuyendo paulatinamente debido al roce, que llamaremos rozamiento entre la bola y el tapete –olvidemos de momento el efecto del choque de la bola con las bandas que se verá más adelante–. Esa modificación de la velocidad implica la existencia de una fuerza, que llamamos fuerza de rozamiento.
Estas fuerzas actúan mediante un
contacto directo con el objeto.
Sin embargo, son conocidas otras fuerzas que actúan sobre un objeto sin que por ello sea necesario un contacto con el mismo. Estas fuerzas actúan
a distancia.
- - Así, cuando lanzamos un cuerpo hacia arriba desde cualquier punto en un entorno próximo a la Tierra, vemos cómo su velocidad disminuye hasta que, en un instante dado, cuando alcanza su máxima altura, se detiene y vuelve hacia abajo. Hay una acción que actúa sobre el cuerpo debido a la existencia de la Tierra, que no está contacto con el cuerpo mientras permanece en el aire, es decir, que se ejerce a distancia, a esa fuerza la llamamos fuerza gravitatoria o más comúnmente peso, aunque no tienen porqué ser exactamente iguales –véase en gravitación la diferencia entre fuerza gravitatoria y peso–.
- - Si frotamos un bolígrafo de plástico contra un jersey de lana, o contra el pelo, y lo acercamos a unos trocitos de papel, observamos que éstos se levantan, tratando de acercarse al bolígrafo. Se está ejerciendo una acción debido a la electrización local –allí donde rozó con la lana y a la cual cedió los electrones de las moléculas de la superficie– del bolígrafo el cual atrae los electrones superficiales, mejor los de los cortes desgarrados, de los trocitos de papel. La acción se ejerce sin que el bolígrafo y los papelitos estén en contacto, se ejerce a distancia.
- - Colocando un imán en el camino de una bola de acero, sin que llegue a tocarla, observamos una modificación de la dirección del vector velocidad, es decir, un cambio de la dirección de la trayectoria. Estos cambios son debidos a las propiedades magnéticas que poseen algunos materiales y son fuerzas que también se ejercen a distancia.
Llamaremos, pues, fuerza a la causa de la variación del vector velocidad de un sistema
puntual. Esta causa puede ser única o el resultado de varias acciones que no se anulan.
También podemos definir la fuerza como la causa de la deformación de un sistema.
Deformación de un sistema
Frecuentemente, un sistema se encuentra sometido simultáneamente a la acción de varias fuerzas exteriores al mismo lo cual nos impide conocer los efectos debidos a la acción de una sola de entre ellas.
Cuando un sistema se encuentra sometido a acciones que se compensan entre sí, no es sencillo poner en evidencia cada una de las acciones por medio de la variación de su velocidad.
- - Hemos hecho referencia a Hooke que ideó un procedimiento para medir la constante de elasticidad de un resorte – Véase Ley de Hooke –. Se observa que si colgamos un objeto de un resorte, el cuerpo cae, pero alarga el resorte, lo deforma, y aparece una fuerza que se opone a tal deformación, que trata de recuperar su forma inicial. Llega un momento en que el peso del cuerpo y la fuerza recuperadora del resorte se igualan y el cuerpo se detiene suspendido del resorte. La velocidad del cuerpo ya no varía. El cuerpo se encuentra en equilibrio.

Explicación gráfica de la Ley de Hooke
Ejemplo 1: Fuerzas que se compensan
Si disponemos el resorte en posición horizontal, sujeto por los extremos a dos tacos de madera deslizantes y estudiamos qué sucede en los extremos del resorte, se pone de manifiesto la aparición de unas fuerzas que se oponen a cualquier deformación.


Fuerzas recuperadora y deformadora de un resorte, respectivamente
Ejemplos 2 y 3: Efectos diferentes de una misma fuerza
Un jugador de volley-ball al sacar pega con el puño al balón y provoca una variación de su velocidad.
Sin embargo, si en un gimnasio pega con el puño sobre una tabla fijada en el suelo, provoca una deformación en ella.
La misma fuerza puede tener efectos diferentes.
Podemos sostener una pesa con la mano, o colocarla sobre una lámina metálica, deformable, o, finalmente, sobre una mesa de madera. En los tres casos se ejerce una fuerza con sentido opuesto a la fuerza gravitatoria, es decir sentido vertical hacia arriba, pues de lo contrario la pesa seguiría su camino de
caída libre.
Como se ha dicho, el peso de un cuerpo existe en cualquier lugar del entorno de la Tierra. En el primer caso sostenemos la pesa con la mano, impidiendo su caída libre. La fuerza será opuesta al peso. De igual modo, si colocamos la pesa sobre la mesa formada por una fina placa metálica deformable, éste se deformará, pero a medida que vaya aumentando su deformación, la placa metálica se opondrá con más fuerza a la causa de su deformación hasta hacerse igual a ella pero de sentido contrario. En el caso de la mesa de tablero grueso de madera, es indeformable, el tablero ejerce directamente una fuerza igual al peso de la pesa.
Definición de fuerza
Hemos visto en diferentes ejemplos los efectos de una acción ejercida sobre los cuerpos, podremos pues afirmar que
Fuerza de una acción mecánica es todo agente capaz de modificar el estado dinámico de un cuerpo o de producirle una deformación.
Definición de Fuerza
|
Tipos de fuerzas
En primer lugar, podemos clasificar las fuerzas en dos grupos:

Fuerza del viento sobre la vela de un barco.
a) Fuerzas de contacto.
Es necesario un contacto directo con el sistema para que éste sufra sus efectos. Una
fuerza de contacto puede ser ejercida de modo que se extienda a una superficie más o menos amplia. Si la superficie de contacto no es muy amplia podemos considerar la fuerza puntual.
En el caso de la acción del viento sobre la vela habrá una fuerza resultante de la suma de las innumerables acciones de las moléculas del aire. En el caso de la masa sobre una plancha el peso del cuerpo se encuentra repartido entre los puntos de la superficie S.
Sin embargo, si tiramos mediante un cable de una vagoneta, la fuerza será puntual ejercida por el gancho y, además, aparecen las fuerzas de rozamiento de las ruedas de la vagoneta al rodar sobre los raíles.
b) Fuerzas a distancia
Hemos visto algún ejemplo de cómo las interacciones entre los objetos pueden hacerse a distancia, así encontramos
- - Fuerzas de gravitación, tales como el peso. Son debidas a la presencia de dos masas a unas distancias moderadas. A esta interacción se la llama también interacción débil.
- - Fuerzas electromagnéticas, debidas a la presencia de cuerpos en reposo cargados eléctricamente, fuerzas electrostáticas, o a la presencia de imanes o de cargas en movimiento, son las fuerzas magnéticas, a esta interacción se le llama interacción fuerte.
- - Fuerzas nucleares, aparecen a muy corta distancia, entre las partículas elementales que componen el núcleo, y son las fuerzas que le dan cohesión. También se llama interacción superfuerte o supergravedad.
Representación de las fuerzas
En el ejemplo observado, del barco moviéndose por acción del viento, colegimos que existen infinidad de partículas moviéndose todas, aparentemente, en la misma dirección y sentido, si la fuerza del viento permanece constante, entonces podemos representar la acción de cada partícula de viento con una
flecha. Esta fecha tendrá una longitud proporcional a la fuerza del viento, a cuyo valor llamaremos
módulo de la fuerza o
intensidad.
La dirección de las flechas será la de la recta soporte de su movimiento
y su sentido el indicado por la punta de la flecha.
A una tal representación la llamaremos
vectorial, de modo que la acción de cada partícula queda representada por un
vector, que poseerá al menos tres características o parámetros:
módulo o
intensidad,
dirección y
sentido.
Si para representar el fenómeno del viento sólo necesitamos estos tres parámetros diremos que su acción queda representada por
vectores libres. Cualquiera de ellos representa a todos y la suma de todas estas acciones será la fuerza resultante.
Puede ocurrir que estuviéramos impidiendo que la vagoneta se moviera mediante un gancho soldado al cable. En este caso, la fuerza de tracción del cable es fija, no se mueve, y tiene un punto P donde apoya su acción. La fuerza es en este caso un
vector fijo y queda definido al igual que antes por el
módulo o
intensidad, una
recta soporte única –no nos sirven cualquiera de sus paralelas– y
punto de apoyo, qué es donde el cable ejerce su acción.
Sin embargo, si la acción que ejerce el cable es capaz de hacer deslizar la vagoneta, además de aparecer las fuerzas de rozamiento –cuyo tratamiento se hará más adelante– estás se ejercen siempre siguiendo la dirección de los raíles, serán
vectores deslizantes.
En consecuencia, cuanto mayor sea la precisión en la localización y representación de una acción necesitaremos mayor número de parámetros. Así:
- - Vectores libres: módulo, dirección y sentido.
- - Vectores deslizantes: módulo o intensidad, dirección, recta soporte y sentido sobre la misma.
- - Vectores fijos: módulo o intensidad, dirección, sentido y punto de aplicación.
Unidades de las fuerzas
La unidad de fuerza es el Newton,
1 N, que se define como
la acción que aplicada sobre un cuerpo de 1 kg de masa transmite una variación rectilínea a la velocidad de un metro por segundo en cada segundo.
De la propia definición del Newton se desprende que hemos aceptado las unidades básicas del
Sistema Internacional, es decir,
De masa,
m, el kilogramo,
kg De tiempo,
t, el segundo,
s De longitud,
l – pero también x, y, z o s -, el metro,
m
Cuando encontramos en una ecuación m, se referirá a la magnitud masa, si s, se referirá a la magnitud longitud o espacio sin embargo, si encontramos un número seguido de s, como dato o como resultado, se referirá a la unidad de tiempo, el segundo. Del mismo modo, si lo que encontramos como dato o resultado un número seguido de m, se referirá a la unidad de longitud, el metro.
Estas unidades nos imponen la unidad de medida de las fuerzas. El Newton es unidad pequeña, equivale aproximadamente a la acción que debemos realizar para soportar una masa de 0,00 kg.
Un hombre puede realizar un esfuerzo entre

y

Fuerza de tracción de un automóvil, es alrededor de

Fuerza de una locomotora es de unos

Fuerza de un cohete para lanzar cuerpos al espacio es de

Estas cifras, en la notación científica deberán expresarse como

,

,

,

,

.
Aparatos de Medida de Fuerzas. Dinamómetros
Si analizamos la gráfica que representa el alargamiento de un resorte en función de la masa que suspendemos del mismo
(Véase Ley de Hooke en el estudio del Movimiento Oscilatorio Armónico) , se concluye la ecuación

, o lo que es igual

. Sin embargo si consideramos que cuando

entonces

, siendo

la longitud del resorte suspendido sin que se le aplique ninguna acción, nos queda

. De ese modo podríamos calibrar la fuerza que es necesario aplicar sobre el resorte para que producir sobre éste un alargamiento igual

.
Un
dinamómetro consta esencialmente de un resorte de espiras no yuxtapuestas soldado al centro de la circunferencia de la base de dos cilindros concéntricos. El cilindro interior lleva una escala que señala la fuerza que se ha aplicado cuando estiramos el resorte y el cilindro interior sale fuera.
No todos los dinamómetros sirven para medir cualquier intensidad de la fuerza. Debemos elegir el dinamómetro de modo que las fuerzas que vaya a medir no provoquen un alargamiento tal que supere el límite de elasticidad del resorte, pues a partir de ese momento el resorte deja de ser elástico y ya ni podrá oponerse a futuras deformaciones ni recuperará su longitud inicial.
Composición de fuerzas
Hemos calificado la fuerza como una magnitud vectorial de la que es necesario conocer al menos tres parámetros:
intensidad,
dirección y
sentido, cuanto más se encuentra restringida la libertad de su movimiento se hace preciso el conocimiento de un parámetro adicional, la recta soporte, o ésta y el punto de apoyo.
Veamos la situación de vectores libres. Cuando se aplican dos fuerzas sobre un cuerpo la acción
resultante se obtiene mediante la
suma geométrica de los dos vectores.
Sean los vectores

y

aplicados sobre un cuerpo que consideraremos una masa puntual. El vector
resultante 
se obtiene construyendo un paralelogramo con los dos vectores o con sendos segmentos iguales y paralelos a ellos. La resultante es la diagonal al paralelogramo así construido que une el origen de los dos vectores con el vértice opuesto.
Es de todo punto evidente que, salvo en el caso de dos vectores perpendiculares entre sí, esta forma de sumar vectores no resulta sencilla.
Existe un procedimiento más sencillo que pasa por la
descomposición ortogonal de ambos vectores.
Descomposición de un vector en dos componentes
Un vector puede considerarse como la suma de dos vectores inexistentes pero que nos permitirán determinar la intensidad del mismo.
Para descomponerlo en dos componentes sobre unas direcciones determinadas, elegidas arbitrariamente por nosotros, trazamos por el origen del vector dos rectas en las direcciones elegidas. Por el extremo del vector trazamos sendas rectas paralelas a las anteriores que cortarán a las dos primeras formando un paralelogramo. El vértice del origen del vector será el origen de los dos vectores componentes cuya intensidad vendrá determinada por la longitud de los lados del paralelogramo. Cuando el ángulo definido por esas dos direcciones elegidas es

decimos que se ha hecho una
descomposición ortogonal.
La suma de los vectores

y

será muy fácil de deducir,
sumando las respectivas componentes según los ejes de coordenadas de los dos vectores.
Realizando la misma descomposición vectorial con el vector

obtendremos

y

.
La suma

, se obtiene obteniendo separadamente

y

, sumas fácilmente realizables por tratarse

y

por un lado y

y

, por otro, de vectores de la misma dirección.
Finalmente

Ejercicios de dinámica I II III

Suma vectorial de fuerzas
La fuerza es una cantidad vectorial ya que tiene magnitud específica, dirección y sentido. En los problemas de estática busacamos encontrar la fuerza resultante o descomponer la fuerza en sus componentes.

Determinación de una fuerza resultante
Si tenemos un pasador sobre el cual están actuando dos fuerzas F 1 y F 2, podemos sumarlas para encontrar la fuerza resultante:
FR=F1+F2

Determinación de las componentes de una fuerza
Cuando nosotros conocemos la fuerza resultante y queremos encontrar sus componentes tenemos que: trazar el paralelogramo y después trazar los vectores que lo formarían en los ejes de referecia.

Suma de varias fuerzas
Si se deben sumar varias fuerzas pueden llevarse a cabo mediante aplicaciones sucesivas de la ley de paralelogramo para obtener la fuerza resultante.

|



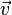 o
o 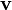 . Su unidad en el
. Su unidad en el 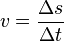



 o
o  y su
y su  .
.
 el móvil lleva una velocidad
el móvil lleva una velocidad  , y fue
, y fue  la velocidad con la que inició el movimiento, es decir la que tuvo en el instante
la velocidad con la que inició el movimiento, es decir la que tuvo en el instante  , tendremos:
, tendremos:

 el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a
el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a  de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir:
de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir:
 (2)
(2) (1)
(1)





 (3)
(3)



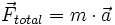
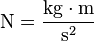






 y
y 



 ,
,  ,
,  ,
,  ,
, .
.
 , o lo que es igual
, o lo que es igual . Sin embargo si consideramos que cuando
. Sin embargo si consideramos que cuando  entonces
entonces  , siendo
, siendo  la longitud del resorte suspendido sin que se le aplique ninguna acción, nos queda
la longitud del resorte suspendido sin que se le aplique ninguna acción, nos queda . De ese modo podríamos calibrar la fuerza que es necesario aplicar sobre el resorte para que producir sobre éste un alargamiento igual
. De ese modo podríamos calibrar la fuerza que es necesario aplicar sobre el resorte para que producir sobre éste un alargamiento igual  .
.
 y
y  aplicados sobre un cuerpo que consideraremos una masa puntual. El vectorresultante
aplicados sobre un cuerpo que consideraremos una masa puntual. El vectorresultante  se obtiene construyendo un paralelogramo con los dos vectores o con sendos segmentos iguales y paralelos a ellos. La resultante es la diagonal al paralelogramo así construido que une el origen de los dos vectores con el vértice opuesto.
se obtiene construyendo un paralelogramo con los dos vectores o con sendos segmentos iguales y paralelos a ellos. La resultante es la diagonal al paralelogramo así construido que une el origen de los dos vectores con el vértice opuesto.
 decimos que se ha hecho una descomposición ortogonal.
decimos que se ha hecho una descomposición ortogonal.

 y
y  .
. , se obtiene obteniendo separadamente
, se obtiene obteniendo separadamente  y
y  , sumas fácilmente realizables por tratarse
, sumas fácilmente realizables por tratarse  y
y  y
y



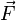 y
y  . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
. Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
No hay comentarios:
Publicar un comentario
EL CONOCIMIENTO ES SABIDURIA ,,, APROVECHALO AL MAXIMO
TIENES ALGUNA DUDA????